Что это — орбита: движение земли, солнца, виды орбит, календарь

Необычные ИСЗ на орбите

Спустя несколько лет после запуска первого ИСЗ СССР, США был выведен спутник связи. Примечательно то, что представляя собой «воздушный шар» из металла, размерами он не уступал 11 этажному дому — 32 метра в диаметре.

Обычно аппараты служат несколько лет, однако существуют и исключения. ИСЗ LAGEOS выведен на орбиту с учетом времени «службы» в 7 миллионов лет. На его борту установлена специальная табличка, которая содержит послание будущим поколениям землян.

«Эстонский парусник» — такое неофициальное название получил аппарат ESTCube. Это первый аппарат с применением технологии «электрического паруса». Технология находится на стадии практических тестов и при успешном результате позволит аппаратам развивать огромное ускорение. Например, аппарат с таким «парусом» доберется до края Солнечной системы всего за 8 лет.

На борту всем известной МКС установлено несколько камер, и любой желающий может почувствовать себя космонавтом и полюбоваться видом нашей планеты с орбиты не выходя из дома. Очень люблю иногда посмотреть на нашу планету из космоса.

Этимология и математическое значение

Женского рода существительного «орбита» является заимствуют от латинского Орбита , обозначающий след колеса.

Первоначально термин орбита — это термин, используемый в математике для обозначения набора точек, пройденных траекторией , то есть параметризованной кривой . Разница между «орбитой» и «траекторией» состоит в том, что траектория выражает эволюцию точки, в то время как орбита является «статическим» понятием. Итак, для траектории орбита — это целое .
жт↦M(т){\ displaystyle f: t \ mapsto M (t)}{M(т)|т∈р}{\ Displaystyle \ {М (т) | т \ в \ mathbb {R} \}}

Таким образом, орбита может иметь любую форму в зависимости от динамики изучаемой системы, но со временем использование этого термина было зарезервировано для замкнутых орбит в астрономии и космонавтике .

Как устроена орбита

Орбита вокруг Земли — явление неоднородное, и астрономия разделяет ее по высоте.

На расстоянии 35 тыс. км находится геостационарная орбита, на которой аппараты вращаются одновременно с Землей, “зависая” на одной долготе.

Эта орбита критически важна для мониторинга погоды, поскольку спутники на ней способны с большой высоты всегда следить за одним и тем же участком планеты.

Как это работает? Пользователь заходит на сайт, чтобы проверить прогноз погоды и смотрит на спутниковые изображения своего населенного пункта. На сайт снимки попали с геостационарной орбиты, на которой находятся специальные спутники. Они каждые пару минут обновляют и отправляют информацию об облаках, водяном паре, ветре, чтобы спрогнозировать погоду в населенном пункте.

Существуют еще несколько видов орбит. Например, “Молния”, имеющая вытянутую эллиптическую форму, где один конец ближе к Земле, чем другой. Вся совокупность орбит хорошо изложена в каталоге NASA.

Наиболее близкая к поверхности — низкая околоземная орбита, расположенная на высоте от 160 до 2 тыс. км. На ней находились все космические станции, а также большая часть спутников — почти 2000.

На этой орбите человек не может выжить без системы жизнеобеспечения, которую используют космонавты для выхода в открытый космос.

Пространство на низкой околоземной орбите не пустое — туда проникают атмосферные газы, которые оказывают на орбитальные объекты хоть и небольшое, но все же влияние, примерно как поток воздуха на пулю, выпущенную из винтовки, разве что в разы слабее. Температура в этом пространстве в среднем составляет около 10 градусов Цельсия. Низкая околоземная орбита — это в принципе не очень далеко от поверхности планеты, так что некоторая схожесть условий не должна вызывать удивления.

На орбитах находятся спутники, работающие во благо человечества. Некоторые спутники работают в течение лет.

Неработающие объекты — это космический мусор. Его устранением занимаются космические компании по всему миру, потому что они представляют опасность для работающих спутников: могут наносить повреждения, которые потом необходимо устранять, либо влиять на точность данных со спутников.

Держим курс: равномерное вращательное движение

Если объект движется с постоянной по величине скоростью по окружности, то такое движение называется равномерным вращательным движением. Примерами такого движения являются движение гоночного автомобиля по круглому треку и стрелки на циферблате часов. На рис. 7.1 показан мяч для игры в гольф, привязанный нитью к шесту и совершающий движение по окружности. Мяч совершает движение с одинаковой по величине скоростью, но с изменяющимся направлением. Потому такое движение мяча называется равномерным вращательным движением.

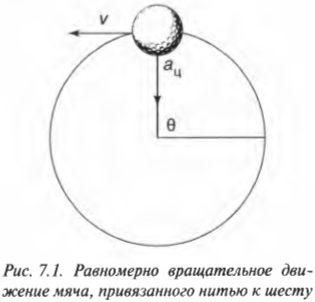
Время, которое требуется мячику (или какому-либо другому объекту), чтобы полностью обогнуть окружность, называется периодом и обозначается символом ​\( T \)​. Период и линейную скорость можно легко связать, если известно пройденное расстояние, т.е. длина окружности ​\( 2\pi r \)​, а точнее ее радиус ​\( r \)​. Итак, линейная скорость мячика ​\( v \)​ равна:

а период вращения ​\( T \)​ равен:

Допустим, что длина нити равна 1 м, а период вращения равен 0,5 с. Чему в таком случае будет равна линейная скорость мячика? Подставим численные значения в одно из предыдущих соотношений и получим:

Итак, мячик вращается с линейной скоростью 13 м/с!

Форма орбиты небесных тел. Космическая скорость

Форма орбит и скорость, с которой по ним передвигаются небесные тела, зависят, в первую очередь, от силы всемирного тяготения. При анализе передвижения небесных тел Солнечной системы во многих случаях пренебрегают их формой и строением, то есть они выступают в качестве материальных точек. Это допустимо из-за того, что расстояние между телами, как правило, во множество раз превышает своих размеров. Если принять небесное тело за материальную точку, то при анализе его перемещения применяется закон всемирного тяготения. Также зачастую рассматривают лишь 2 притягивающихся тела, опуская влияние других.

Пример 1

При исследовании траектории движения Земли вокруг Солнца можно с вероятной точностью предположить, что планета передвигается лишь под действием сил солнечного тяготения

Равно также при исследовании движения искусственного спутника планеты принимается во внимание только тяготение «своей» планеты, при этом опускается не только притяжение других планет, но и солнечное

Замечание 1

Предыдущие упрощения позволили прийти к задаче 2-х тел. Одно из решений данной задачи предложил И. Кеплер. А полное решение сформулировал И. Ньютон, доказавший, что одно из притягивающихся небесных тел обращается вокруг другого по орбите в форме эллипса (или окружности, частного случая эллипса), параболы либо гиперболы. В фокусе данной кривой лежит 2-я точка.

На форму орбиты влияют следующие параметры:

• масса рассматриваемого тела;
• расстояние между ними;
• скорость, с которой одно тело движется по отношению к другому.

Если тело массой m1 (кг) расположено на расстоянии r (м) от тела массой m (кг) и передвигается в данный момент времени со скоростью υ (мс), тогда орбита задается постоянной:

Определение 2

Постоянная тяготения f=6,673·10-11 м3кг-1с-2. Если h − по гиперболической орбите.

Определение 3

Вторая космическая скорость − это наименьшая начальная скорость, которую необходимо сообщить телу, чтобы оно начало движение около поверхности Земли, преодолело земное притяжение и навсегда покинуло планету по параболической орбите. Она равняется 11,2 кмс.

Определение 4

Первой космической скоростью называют наименьшую начальную скорость, которую необходимо сообщить телу, чтобы оно стало искусственным спутником планеты Земля. Она равняется 7,91 кмс.

Большинство тел Солнечной системы перемещается по эллиптическим траекториям движения. Только лишь некоторые маленькие тела Солнечной системы такие, как кометы, вероятно перемещаются по параболическим или гиперболическим траекториям. Таким образом, межпланетные станции отправляются по гиперболической орбите по отношению к Земле; потом они перемещаются по эллиптическим траекториям по отношению к Солнцу в направлении к точке назначения.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Примечания и ссылки

1. и
2. Так , в его Комментарии к трактату Du Ciel по Аристотелю , он пишет:

   —  Симплиций , Комментарии к трактату Аристотеля Duciel , II, 12, 488 и 493.

   .

3. ↑ и См., Например, Encyclopedia Universalis , издание 2002, том 3, статья «Астрономия и астрофизика» ( ISBN  2-85229-550-4 ) , или Notionnaires Universalis — Ideas , ( ISBN  2-85229-562-8 ) , Encyclopedia Universalis France SA, Париж, 2005.
4. «Пополнение словарного запаса космической техники» , Министерство промышленности (Франция) , Пополнение словарного запаса нефтяной, ядерной и космической техники , стр.  33 (по состоянию на 6 апреля 2014 г.)
5. (fr) Люк Дюрье, «Повторное обращение к проблеме двух тел», в Даниэле Бенесте и Клода Фрешле (ред.), Современные методы небесной механики , Гиф-сюр-Иветт, Границы, 2-е изд., 1992, с. 18 ( ISBN  2-86332-091-2 )
6. ↑ и Мишель Капдеру, Спутники: от Кеплера до GPS , Париж / Берлин / Гейдельберг и т. Д., Springer,2012 г., 844  с. , стр.  321-322
7. .

Список используемой литературы

• Ивон Вильярсо, Диссертация по определению орбит планет и комет , Забытые книги,2018 г.( ISBN  978-0-332-62798-4 )
• Мишель Капдеру, спутники: от Кеплера до GPS , Париж / Берлин / Гейдельберг и т. Д., Springer,2012 г., 844  с.

Орбита Земли

Орбита нашей планеты представляет собой эллипс, в одном краю которого находится Солнце. Путь до Земли от Солнца на протяжении года изменяется, начиная от 147 млн км до 152 млн км. Орбита длинная, около 930 млн км. Наша планета двигается с запада на восток со скоростью примерно 30 км/с. Все расстояние она преодолевает за 365 дней 6 ч. 9 мин. и 9 с. Это время получило название звездного года.

Еще есть понятие тропического года, которое предполагает временное расстояние между определенными последовательными перемещениями Солнца через точку весеннего равноденствия. Этот временный промежуток равен 365 дням 5 ч. 48 мин. и 46 с.

Изучение Солнечной системы

Долгое время человечество было убеждено, что все звёзды и планеты вращаются вокруг Земли. Система мира с неподвижной Землёй в центре была разработана греческим учёным Птолемеем во 2 веке до нашей эры и просуществовала более полутора тысяч лет. 

В 1453 году польский астроном Николай Коперник доказал, что Земля, как и другие планеты (на тот момент их было известно шесть), вращаются вокруг Солнца. Однако вплоть до XVII века церковь считала это учение ересью и боролась с его последователями. 

Одним из них был итальянский монах Джордано Бруно. В 1584 году он опубликовал исследование, в котором утверждал, что Вселенная бесконечна, а Солнце подобно остальным звёздам, просто находится гораздо ближе к Земле. Бруно был схвачен инквизицией и приговорён к сожжению на костре как еретик. 

Другим последователем Коперника стал итальянский учёный Галилео Галилей. Он создал первый телескоп, который позволил увидеть кратеры Луны, пятна на Солнце, открыть четыре спутника Юпитера и установить, что планеты вращаются вокруг своей оси. Чтобы не повторить судьбу Бруно, Галилей был вынужден отречься от своих идей.

В XVII веке немецкий астроном Иоганн Кеплер открыл законы движения планет — ему удалось установить связь между скоростью вращения планеты и её расстоянием от Солнца. Его идеи воспринял знаменитый английский физик Исаак Ньютон, создатель теории всемирного тяготения. 

В XVIII—XIX веках открытия в области оптики позволили создать более мощные телескопы, которые позволили учёным узнать больше о солнечной системе. Были открыты планеты Уран и Нептун. 

В 1951 году Советский Союз вывел на орбиту Земли первый искусственный спутник. С этого момента началась Космическая эра — эпоха практического изучения солнечной системы. 

В 1961 году Юрий Гагарин стал первым человеком, побывавшем в космосе, а в 1969 году космический корабль «Аполлон-11» доставил людей на Луну. 

В 1970-х годах Советский Союз и США запустили несколько десятков аппаратов для исследования Марса, Венеры и Меркурия, а запущенные в 1980-х аппараты «Вояджер-1» и «Вояджер-2» позволили получить данные о дальних планетах — Юпитере, Сатурне, Уране, Нептуне и их спутниках. Большую роль в изучении солнечной системы сыграл вывод на орбиту Земли космического телескопа «Хаббл» в 1990 году. 

В нынешнем десятилетии космические агентства разных стран планируют пилотируемый полёт на Марс. Экспедиция на другую планету станет величайшим событием в истории освоения солнечной системы. И всё же пока человечество находится в самом начале пути изучения космоса.

Методы [ править ]

При определении орбиты необходимо учитывать, что на кажущееся небесное движение тела влияет собственное движение наблюдателя. Например, наблюдатель на Земле, отслеживающий астероид, должен учитывать движение Земли вокруг Солнца , вращение Земли и местную широту и долготу наблюдателя, поскольку они влияют на видимое положение тела.

Ключевое наблюдение состоит в том, что (в точном приближении) все объекты движутся по орбитам, которые представляют собой конические сечения , с притягивающим телом (таким как Солнце или Земля) в главном фокусе , и что орбита лежит в фиксированной плоскости. Все векторы, проведенные от притягивающего тела к телу в разные моменты времени, будут лежать в плоскости орбиты .

Если положение и скорость относительно наблюдателя доступны (как в случае с радиолокационными наблюдениями), эти данные наблюдений могут быть скорректированы с помощью известного положения и скорости наблюдателя относительно притягивающего тела во время наблюдения. Это дает положение и скорость относительно притягивающего тела. Если доступны два таких наблюдения, а также разница во времени между ними, орбиту можно определить с помощью метода Ламберта, изобретенного в 18 веке. Подробнее см . Проблему Ламберта .

Даже если информация о расстоянии недоступна, орбита все равно может быть определена, если были сделаны три или более наблюдений прямого восхождения и склонения тела. Метод Гаусса , прославившийся благодаря его «восстановлению» в 1801 году первой потерянной малой планеты , Цереры , впоследствии был доработан.

Одно из применений — определение масс астероидов динамическим методом . В этой процедуре метод Гаусса используется дважды, как до, так и после тесного взаимодействия двух астероидов. После определения обеих орбит можно определить массу одного или обоих астероидов. [ необходима цитата ]

Космический телескоп «Хаббл»

Телескоп «Хаббл», названный в честь Эдвина Хаббла, был запущен на орбиту 24 апреля 1990 года. Это совместный проект NASA и Европейского космического агентства, задуманный как обсерватория общего назначения для исследования Вселенной в видимом, ультрафиолетовом и инфракрасном диапазонах волн. Входит в число NASA.

Телескоп «Хаббл»

(Фото: NASA)

20 мая 1990 года телескоп сделал первую фотографию звездного скопления NGC 3532.

Слева — снимок, сделанный из обсерватории Лас Кампанас, Чили. Справа — часть первого изображения «Хаббла»

(Фото: NASA, ESA, and STScI)

«Хаббл» вращается вокруг Земли на высоте около 540 км и наклонен на 28,5 градусов к экватору. Чтобы совершить один оборот, ему требуется 95 минут.

Орбитальный телескоп провел более 1 млн наблюдений и предоставил данные, которые астрономы использовали, чтобы написать свыше 18 тыс. рецензируемых научных публикаций (от формирования планет до гигантских черных дыр). Эти документы упоминались в других публикациях более 900 тыс. раз.

Чем известен «Хаббл»

• Благодаря изучению пульсирующих звезд удалось определить возраст нашей Вселенной — 13,8 млрд лет.
• В январе 1992 года астрономы подтвердили существование планет за пределами солнечной системы.
• Телескоп зафиксировал редкое явление — столкновение кометы Шумейкера-Леви 9 с Юпитером в 1994 году. Это первые в истории фотографии столкновения двух объектов Солнечной системы.

Серия снимков, сделанных с помощью космического телескопа «Хаббл» NASA, показывает эволюцию области падения кометы Шумейкера-Леви

(Фото: H. Hammel, MIT and NASA)

• Телескоп детально зафиксировал эволюцию погоды Юпитера, в том числе редкий шторм возле экватора планеты.
• «Хаббл» показал Плутон впервые с момента открытия планеты в 1930 году.
• Аппарат сфотографировал шлейф газа и пыли высотой 400 км в результате извержения вулкана Ио, самой большой внутренней луны Юпитера.

Изображения сделаны 14 февраля 2007 года. На левом видны оранжевые овальные отложения серы вокруг вулкана Пеле. На правом изображении виден большой шлейф, поднимающийся над поверхностью, недалеко от северного полюса

(Фото: NASA, ESA, and J. Spencer (SwRI))

• Подтвердил предположения о наличии сверхмассивных черных дыр в ядрах Галактик.
• Нашел самый далекий из известных на сегодня космических объектов — галактику GN-z11. Сейчас мы видим ее такой, какой она была 13,4 млрд лет назад.

Галактика GN-z11, показанная на вставке, видна в прошлом на 13,4 млрд лет, всего через 400 млн лет после Большого взрыва, когда возраст Вселенной составлял всего 3% от ее нынешнего возраста. Учитывая расширение Вселенной, сейчас на деле она находится в 32 млрд световых лет от нас

(Фото: NASA, ESA, P. Oesch (Yale University))

• Подтвердил существование на спутнике Юпитера Ганимеде огромного подземного океана под 150-километровой толщей льда. На основании этого открытия астрономы внесли крупнейший спутник в Солнечной системе в список возможных кандидатов на поиск жизненных форм.
• Обнаружил водяной пар на экзопланете K2-18b из обитаемой зоны, а также первую подтвержденную межзвездную комету 2I/Borisov.

13 июня 2021 года компьютер, отвечающий за научное оборудование «Хаббла», перестал реагировать на команды с Земли. Устранить поломку инженерно-научной группе, обслуживающей телескоп, удалось только к 16 июля 2021 года.

У орбитального «Хаббла» есть два аккаунта в Twitter — Hubble NASA и Hubble ESA, два официальных YouTube канала — NASA и ESA, а также аккаунты в Instagram и .

Посвященный «Хабблу» ролик NASA

Изображения и данные, полученные с космического телескопа «Хаббл», показывают галактики такими, какими они были миллиарды лет назад.

Расчет

Эксцентриситет орбиты может быть вычислен из орбитальных векторов состояния , как этого вектора эксцентриситета :

езнак равно|е|{\ Displaystyle е = \ влево | \ mathbf {е} \ вправо |}

куда:

e — вектор эксцентриситета ( «вектор Гамильтона» ).

Для эллиптических орбит он также может быть рассчитан на основе перицентра и апоапсиса, поскольку и где а — длина большой полуоси , среднее геометрическое и среднее по времени расстояние.
рпзнак равноа(1-е){\ Displaystyle \, г _ {\ текст {p}} = а \, (1-е) \,}разнак равноа(1+е),{\ Displaystyle \, г _ {\ текст {а}} = а \, (1 + е) \ ,,}

езнак равнора-рпра+рпзнак равнорарп-1рарп+1знак равно1-2рарп+1{\ displaystyle {\ begin {align} e & = {\ frac {r _ {\ text {a}} — r _ {\ text {p}}} {r _ {\ text {a}} + r _ {\ text {p} }}} \\\, \\ & = {\ frac {r _ {\ text {a}} / r _ {\ text {p}} — 1} {r _ {\ text {a}} / r _ {\ text { p}} + 1}} \\\, \\ & = 1 — {\ frac {2} {\; {\ frac {r _ {\ text {a}}} {r _ {\ text {p}}}} +1 \;}} \ end {выровнено}}}

куда:

• r _a — радиус в апоапсисе (он же «апофокус», «афелий», «апогей», то есть самое дальнее расстояние от орбиты до центра масс системы, который является фокусом эллипса).
• r _p — радиус в перицентре (также известный как «перифокус» и т. д., ближайшее расстояние).

Эксцентриситет эллиптической орбиты также можно использовать для получения отношения радиуса перицентра к радиусу апоапсиса :

рарпзнак равноа(1+е)а(1-е)знак равно1+е1-е{\ displaystyle {\ frac {r _ {\ text {a}}} {r _ {\ text {p}}}} = {\ frac {\, a \, (1 + e) ​​\,} {\, a \ , (1-e) \,}} = {\ frac {1 + e} {1-e}}}

Для Земли эксцентриситет орбиты e ≈ 0,01671, апоапсис — это афелий, а периапсис — это перигелий относительно Солнца.

Для годовой орбитальной траектории Земли отношение наибольшего радиуса ( r _a ) / наименьшего радиуса ( r _p ) составляетрарпзнак равно1+е1-е ≈ 1.03399.{\ displaystyle {\ frac {\, r _ {\ text {a}} \,} {r _ {\ text {p}}}} = {\ frac {\, 1 + e \,} {1-e}} {\ text {≈ 1.03399.}}}

Примеры

График изменения эксцентриситета орбиты Меркурия , Венеры , Земли и Марса в течение следующих 50 000 лет. Стрелки указывают на разные шкалы, поскольку эксцентриситет Меркурия и Марса намного больше, чем у Венеры и Земли. 0 точка на этом графике — 2007 год.

Эксцентриситет тел Солнечной системы

Объект	эксцентриситет
Тритон	0,000 02
Венера	0,006 8
Нептун	0,008 6
Земля	0,016 7
Титан	0,028 8
Уран	0,047 2
Юпитер	0,048 4
Сатурн	0,054 1
Луна	0,054 9
1 Церера	0,075 8
4 Веста	0,088 7
Марс	0,093 4
10 Гигиея	0,114 6
Makemake	0,155 9
Хаумеа	0,188 7
Меркурий	0,205 6
2 Паллада	0,231 3
Плутон	0,248 8
3 Юнона	0,255 5
324 Бамберга	0,340
Эрис	0,440 7
Нереида	0,750 7
Седна	0,854 9
Комета Галлея	0,967 1
Комета Хейла-Боппа	0,995 1
Комета Икея-Секи	0,999 9
C / 1980 E1	1.057
ʻOumuamua	1,20
C / 2019 Q4 (Борисов)	3.5

Эксцентриситет земной орбиты в настоящее время составляет около 0,0167; его орбита почти круглая. У Венеры и Нептуна эксцентриситеты еще меньше. За сотни тысяч лет эксцентриситет земной орбиты изменяется от почти 0,0034 до почти 0,058 в результате гравитационного притяжения планет.

В таблице перечислены значения для всех планет и карликовых планет, а также выбранных астероидов, комет и лун. У Меркурия самый большой эксцентриситет орбиты из всех планет Солнечной системы ( e = 0,2056). Такого эксцентриситета достаточно, чтобы Меркурий получил вдвое больше солнечного излучения в перигелии по сравнению с афелием. Перед понижением статуса планеты в 2006 году Плутон считался планетой с наиболее эксцентричной орбитой ( e = 0,248). Другие транснептуновые объекты имеют значительный эксцентриситет, особенно карликовая планета Эрида (0,44). Еще дальше, Седна , имеет чрезвычайно высокий эксцентриситет0,855 из-за предполагаемого афелия 937 а.е. и перигелия около 76 а.е.

Большинство астероидов Солнечной системы имеют эксцентриситет орбиты от 0 до 0,35 со средним значением 0,17. Их сравнительно высокие эксцентриситеты, вероятно, связаны с влиянием Юпитера и прошлыми столкновениями.

Значение Луны составляет 0,0549, это самый эксцентричный из больших спутников Солнечной системы. Четыре галилеевых луны имеют эксцентриситет менее 0,01. Самый большой спутник Нептуна Тритон имеет эксцентриситет1,6 × 10 −5 (0,000 016 ), наименьший эксцентриситет любой известной луны в Солнечной системе; его орбита настолько близка к идеальному кругу, насколько это возможно в настоящее время. Однако спутники меньшего размера, особенно спутники неправильной формы , могут иметь значительный эксцентриситет, например, третья по величине луна Нептуна Нереида (0,75).

Кометы имеют очень разные значения эксцентриситета. Периодические кометы имеют эксцентриситет в основном от 0,2 до 0,7, но некоторые из них имеют сильно эксцентричные эллиптические орбиты с эксцентриситетом чуть меньше 1; например, комета Галлея имеет значение 0,967. Непериодические кометы движутся по почти параболическим орбитам и поэтому имеют эксцентриситет даже ближе к 1. Примеры включают комету Хейла – Боппа со значением 0,995 и комету C / 2006 P1 (МакНота) со значением1.000 019 . Поскольку значение Хейла – Боппа меньше 1, его орбита эллиптическая, и он вернется. Комета МакНота движется по гиперболической орбите, пока находится под влиянием планет, но все еще привязана к Солнцу с периодом обращения около 10 5 лет. Комета C / 1980 E1 имеет самый большой эксцентриситет из всех известных гиперболических комет солнечного происхождения с эксцентриситетом 1,057 и в конце концов покинет Солнечную систему .

`Оумуамуа — первый обнаруженный межзвездный объект, проходящий через Солнечную систему. Его орбитальный эксцентриситет 1,20 указывает на то, что Оумуамуа никогда не был гравитационно привязан к Солнцу. Он был обнаружен в 0,2 а.е. (30 000 000 км; 19 000 000 миль) от Земли и имеет диаметр примерно 200 метров. Он имеет межзвездную скорость (скорость на бесконечности) 26,33 км / с (58 900 миль в час).

Классификация орбит искусственных спутников

Наземный трек спутника на солнечно-синхронной орбите (вверху) и орбите Молнии (внизу).

Пять точек Лагранжа системы Земля-Солнце: на практике используются только L1 и L2.

Орбиты искусственных спутников можно классифицировать по разным критериям:

Высота (круговая орбита)

Когда орбита почти круговая, она называется низкой орбитой (LEO, от англ. Low Earth Orbit ), если ее высота меньше 1500  км , средней орбитой (MEO, от Medium Earth Orbit ), если она составляет от 1500 до 20000  км , и высокой. орбита за пределами. Наиболее распространенная высокая орбита, поскольку спутник может постоянно находиться над одним и тем же регионом Земли, находится на высоте 36 000 км и называется геостационарной орбитой (или GEO от английского Geostationnary Earth Orbit ). Для этого требуется, чтобы наклонение орбиты было 0 °. Орбита на этой высоте с нулевой орбитой или без нее является геосинхронной орбитой . Большинство спутников находятся на круговой орбите вокруг Земли или находятся на низкой орбите ( спутниковое наблюдение Земли , разведывательный спутник ) на средней орбите в 20 000 км ( спутниковая навигация ) на геостационарной орбите ( телекоммуникационный спутник , метеорологический спутник ).

Высота (эллиптическая орбита)

Среди высоких эллиптических орбит (или HEO от английского High Earth Orbit ) мы находим орбиты, отвечающие очень точным целям, такие как орбита Молнии, обеспечивающая лучшую видимость с высоких широт, чем геостационарная орбита или орбита тундры, которая является вариантом. Орбита передачи (или ГТО означает геопереходную орбиту ) представляет собой переходную орбиту которого апогей составляет 36000 км, который используется с помощью спутников , которые должны быть размещены на геостационарной орбите.

Частный случай орбит вокруг точек Лагранжа.

Орбита вокруг точки Лагранжа (область пространства, где уравновешивается гравитационное влияние двух небесных тел) представляет собой гало- орбиту (или орбиту Лиссажу , ссылаясь на ее форму, которая напоминает кривую Лиссажу ) и обозначается L1LO (L1 Lissajous Orbit ) или L2LO, L1 и L2 — две точки Лагранжа системы Земля-Солнце, используемые, в частности, спутниками для астрономических наблюдений или изучения Солнца. Путешествие по этим нестабильным орбитам занимает около 200 дней и требует регулярных корректирующих маневров.

Орбитальный наклон

В зависимости от значения угла наклона орбиты i мы говорим об экваториальной орбите (i = 0 °), квазиэкваториальной орбите (i <10 °), полярной или квазиполярной орбите (i близкой к 90 °). Если наклонение орбиты меньше или равно 90 °, что характерно для большинства спутников, орбита называется прямой (или прямой), в противном случае — ретроградной.

Свойство

Спутники на геостационарной орбите, в фиксированном положении над Землей, иногда противопоставляются движущимся спутникам . В категории полярных орбит широко используемая орбита, солнечно-синхронная орбита , характеризуется движением своей орбитальной плоскости, которая вращается под действием узловой прецессии синхронно с движением Земли вокруг Солнца. Спутник этого типа всегда проходит снова в одно и то же солнечное время над освещенной областью. Фазированная орбита является категорией солнечно-синхронной орбиты характеризуется тем , что спутник после определенного числа оборотов проходит точно над одной и той же точкой.

Прочие обозначения, не связанные с характеристиками орбиты

Космический аппарат может быть переведен на резервную орбиту (обычно на низкую орбиту), чтобы достичь выгодной позиции для выполнения следующего орбитального маневра. Дрейф орбита является переходной орбитой , пройденными спутниками пассивно достигают свое конечное положение на геостационарной орбите. Наконец, по окончании срока службы спутник помещается на орбиту кладбища (или орбиту отходов), чтобы не оказаться на пути активных спутников.

Расстояние от Солнца до Земли

Этот параметр зависит от точки нахождения нашей планеты в пространстве. Расстояние равно:

• в перигелии (ближайшей точке к Солнцу) — 147,1 млн км;
• в афелии (самой удаленной от светила позиции, называемой также апогелием) — 152,1 млн км.

Для приблизительных расчетов принято среднее значение удаленности (орбитальной полуоси) — 149,6 млн. км. Эта величина является основной мерой измерения расстояний в космосе — 1 астрономической единицей (а.е.). С ее помощью определять длину чего угодно в космическом пространстве проще, чем высчитывать абсолютные значения.

Среднее расстояние от Земли до Солнца равняется 0,000004848 парсеков, или примерно 150 млн км. Credit: telegramfor.me.

Эта мера была принята еще в Средние века, но поначалу не имела никакого численного значения — все линейные расстояния выражались в условной дистанции между Землей и Солнцем. Только в 1672 г. европейский ученый Дж. Кассини впервые оценил орбитальный радиус Земли в 140 млн км. Это значение было уточнено только советскими астрономами в 1961 г. Полученное ими значение — 149,5993 млн км с погрешностью +/- 2000 км.

Точку перигелия наша планета проходит в промежутке с 2 до 5 января каждого года. И хотя солнечного тепла на поверхность планеты в этот период попадает больше, в северном полушарии в это время длится зима. В афелии Земля оказывается между 3 и 7 июля, минимум света и тепла от центральной звезды не мешает продолжаться лету во всех регионах севернее экватора.

Траектория движения планеты вокруг Солнца. Credit: wikiwand.com.